Nearest Neighbor Indexes: What Are IVFFlat Indexes in Pgvector and How Do They Work

The rising popularity of ChatGPT, OpenAI, and applications of Large Language Models (LLMs) has brought the concept of approximate nearest neighbor search (ANN) to the forefront and sparked a renewed interest in vector databases due to the use of embeddings. Embeddings are mathematical representations of phrases that capture the semantic meaning as a vector of numerical values.

What makes this representation fascinating—and useful—is that phrases with similar meanings will have similar vector representations, meaning the distance between their respective vectors will be small. We recently discussed one application of these embeddings, retrieval-augmented generation—augmenting base LLMs with knowledge that it wasn’t trained on—but there are numerous other applications as well.

Semantic similarity search

One common application of embeddings is precisely semantic similarity search. The basic concept behind this approach is that if I have a knowledge library consisting of various phrases and I receive a question from a user, I can locate the most relevant information in my library by finding the data that is most similar to the user's query.

This is in contrast to lexical or full-text search, which only returns exact matches for the query. The remarkable aspect of this technique is that, since the embeddings represent the semantics of the phrase rather than its specific wording, I can find pertinent information even if it is expressed using completely different words!

The challenge of speed at scale

Semantic similarity search involves calculating an embedding for the user's question and then searching through my library to find the K most relevant items related to that question—these are the K items whose embeddings are closest to that of the question. However, when dealing with a large library, it becomes crucial to perform this search efficiently and swiftly. In the realm of vector databases, this problem is referred to as "Finding the k nearest neighbors" (KNN).

This post discusses a method to enhance the speed of this search when utilizing PostgreSQL and pgvector for storing vector embeddings: the Inverted File Flat (IVFFlat) algorithm for approximate nearest neighbor search. We’ll cover why IVFFlat is useful, how it works, and best practices for using it in pgvector for fast similarity search over embeddings vectors.

Let’s go!

P.S. If you’re looking for the fastest vector search index on PostgreSQL, check out pgvectorscale.

What Are IVFFlat Indexes?

IVFFlat indexes, short for Inverted File with Flat Compression, are a type of vector index used in PostgreSQL's pgvector extension to speed up similarity searches to find vectors that are close to a given query. This index type uses approximate nearest neighbor search (ANNS) to provide fast searches.  

These indexes work by dividing the vectors into multiple lists, known as clusters. Each cluster represents a region of similar vectors, and an inverted index is built to map each region to its corresponding vectors. When a query comes in, the nearest clusters to the query are identified and only the vectors in those clusters are searched. Thus, this approach significantly reduces the scope of similarity searches by excluding all the vectors that are not in the clusters that are close to the query.

Why Use the IVFFlat Index in Pgvector

Searching for the k-nearest neighbors is not a novel problem for PostgreSQL. PostGIS, a PostgreSQL extension for handling location data, stores its data points as two-dimensional vectors (longitude and latitude). Locating nearby locations is a crucial query in that domain.

PostGIS tackles this challenge by employing an index known as an R-Tree, which yields precise results for k-nearest neighbor queries. Similar techniques, such as KD-Trees and Ball Trees, are also employed for this type of search in other databases.

"The curse of dimensionality"

However, there's a catch. These approaches cease to be effective when dealing with data larger than approximately 10 dimensions due to the "curse of dimensionality." Cue the ominous music! Essentially, as you add more dimensions, the available space increases exponentially, resulting in exponentially sparser data. This reduced density renders existing indexing techniques, like the aforementioned R-Tree, KD-Trees, and Ball Trees, which rely on partitioning the space, ineffective. (To learn more, I suggest these two videos: 1, 2).

Given that embeddings often consist of more than a thousand dimensions—OpenAI’s are 1,536—new techniques had to be developed. There are no known exact algorithms for efficiently searching in such high-dimensional spaces. Nevertheless, there are excellent approximate algorithms that fall into the category of approximate nearest neighbor algorithms. Numerous such algorithms exist, but in this article, we will delve into the Inverted File Flat or IVFFlat algorithm, which is provided by pgvector.

How the IVFFlat Index Works in pgvector

How IVFFlat divides the space

To gain an intuitive understanding of how IVFFlat works, let's consider a set of vectors represented in a two-dimensional space as the following points:

In the IVFFlat algorithm, the first step involves applying k-means clustering to the vectors to find cluster centroids. In the case of the given vectors, let's assume we perform k-means clustering and identify four clusters with the following centroids.

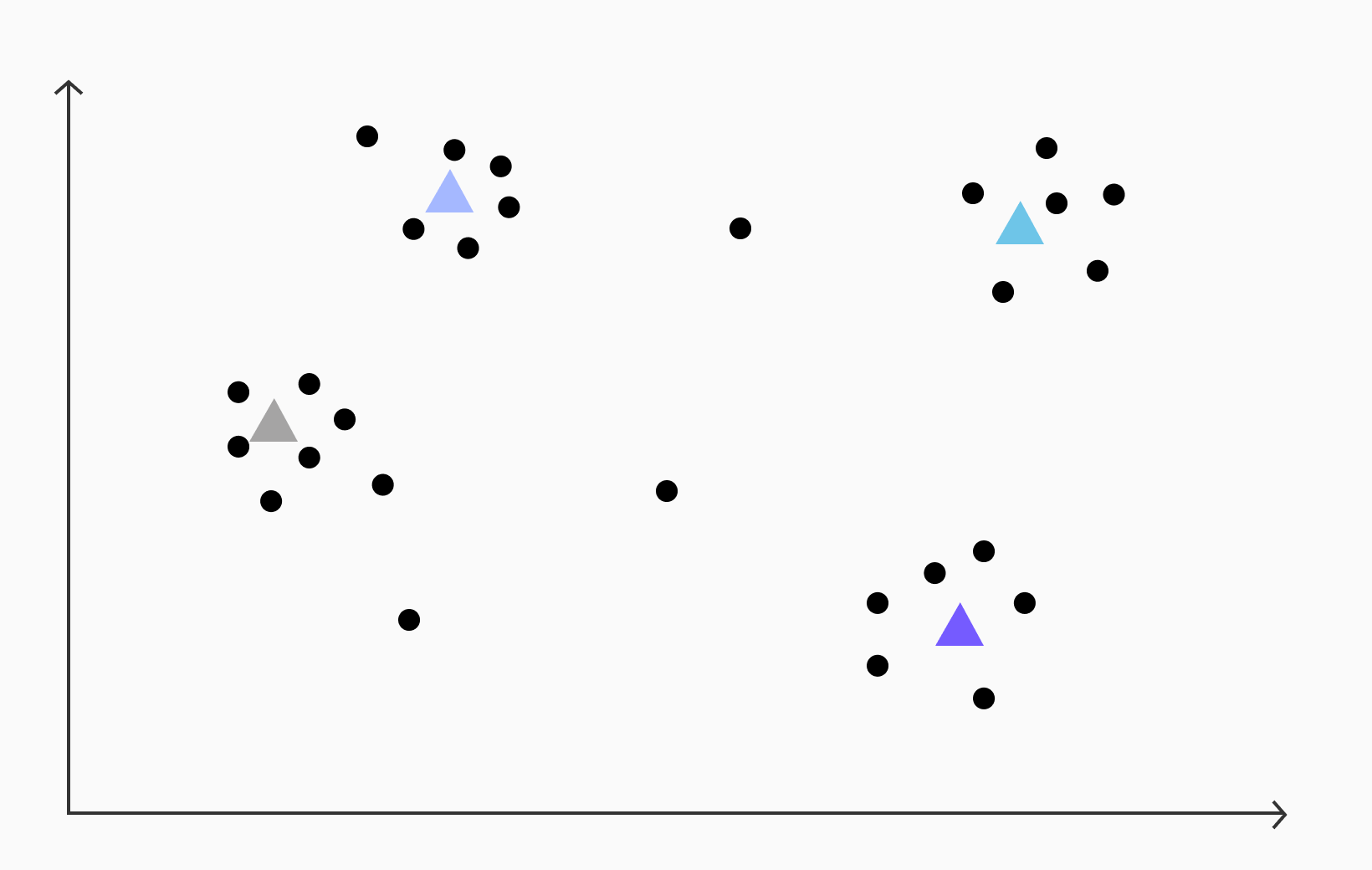
After computing the centroids, the next step is to assign each vector to its nearest centroid. This is accomplished by calculating the distance between the vector and each centroid and selecting the centroid with the smallest distance as the closest one. This process conceptually maps each point in space to the closest centroid based on proximity.

By establishing this mapping, the space becomes divided into distinct regions surrounding each centroid (technically, this kind of division is called a Voronoi Diagram). Each region represents a cluster of vectors that exhibit similar characteristics or are close in semantic meaning.

This division enables efficient organization and retrieval of approximate nearest neighbors during subsequent search operations, as vectors within the same region are likely to be more similar to each other than those in different regions.

Building the IVFFlat index in pgvector

IVFFlat proceeds to create an inverted index that maps each centroid to the set of vectors within the corresponding region. In pseudocode, the index can be represented as follows:

inverted_index = {
  centroid_1: [vector_1, vector_2, ...],
  centroid_2: [vector_3, vector_4, ...],
  centroid_3: [vector_5, vector_6, ...],
  ...
}

Here, each centroid serves as a key in the inverted index, and the corresponding value is a list of vectors that belong to the region associated with that centroid. This index structure allows for efficient retrieval of vectors in a region when performing similarity searches.

Searching the IVFFlat index in pgvector

Let's imagine we have a query for the nearest neighbors to a vector represented by a question mark, as shown below:

To find the approximate nearest neighbors using IVFFlat, the algorithm operates under the assumption that the nearest vectors will be located in the same region as the query vector. Based on this assumption, IVFFlat employs the following steps:

1. Calculate the distance between the query vector (red question mark) and each centroid in the index.
2. Select the centroid with the smallest distance as the closest centroid to the query (the blue centroid in this example).
3. Retrieve the vectors associated with the region corresponding to the closest centroid from the inverted index.
4. Compute the distances between the query vector and each of the vectors in the retrieved set.
5. Select the K vectors with the smallest distances as the approximate nearest neighbors to the query.
   

The use of the index in IVFFlat accelerates the search process by restricting the search to the region associated with the closest centroid. This results in a significant reduction in the number of vectors that need to be examined during the search. Specifically, if we have C clusters (centroids), on average, we can reduce the number of vectors to search by a factor of 1/C.

Searching at the edge

The assumption that the nearest vectors will be found in the same region as the query vector can introduce recall errors in IVFFlat. Consider the following query:

From visual inspection, it becomes apparent that one of the light-blue vectors is closer to the query vector than any of the dark-blue vectors, despite the query vector falling within the dark-blue region. This illustrates a potential error in assuming that the nearest vectors will always be found within the same region as the query vector.

To mitigate this type of error, one approach is to search not only the region of the closest centroid but also the regions of the next closest R centroids. This approach expands the search scope and improves the chances of finding the true nearest neighbors.

In pgvector, this functionality is implemented through the `probes` parameter, which specifies the number of centroids to consider during the search, as described below.

Parameters for Pgvector’s IVFFlat Implementation

In the implementation of IVFFlat in pgvector, two key parameters are exposed: lists and probes.

Lists parameter in pgvector

The lists parameter determines the number of clusters created during index building (It’s called lists because each centroid has a list of vectors in its region). Increasing this parameter reduces the number of vectors in each list and results in smaller regions.

It offers the following trade-offs to consider:

• Higher lists value speeds up queries by reducing the search space during query time.
• However, it also decreases the region size, which can lead to more recall errors by excluding some points.
• Additionally, more distance comparisons are required to find the closest centroid during step one of the query process.
  

Here are some recommendations for setting the lists parameter:

• For datasets with less than one million rows, use lists = rows / 1000.
• For datasets with more than one million rows, use lists = sqrt(rows).
• It is generally advisable to have at least 10 clusters.

Probes parameter in pgvector

The probes parameter is a query-time parameter that determines the number of regions to consider during a query. By default, only the region corresponding to the closest centroid is searched. By increasing the probes parameter, more regions can be searched to improve recall at the cost of query speed.

The recommended value for the probes parameter is probes = sqrt(lists).

Using IVFFlat in Pgvector

Creating an index

When creating an index, it is advisable to have existing data in the table, as it will be utilized by k-means to derive the centroids of the clusters.

The index in pgvector offers three different methods to calculate the distance between vectors: L2, inner product, and cosine. It is essential to select the same method for both the index creation and query operations. The following table illustrates the query operators and their corresponding index methods:

Note: OpenAI recommends cosine distance for its embeddings.

To create an index in pgvector using IVFFlat, you can use a statement using the following form:

CREATE INDEX ON <table name> USING ivfflat (<column name> <index method>) WITH (lists = <lists parameter>);

Replace <table name> with the name of your table and <column name> with the name of the column that contains the vector type.

For example, if our table is named embeddings and our embedding vectors are in a column named embedding, we can create an IVFFlat index as follows:

CREATE INDEX ON embeddings USING ivfflat (embedding vector_cosine_ops) WITH (lists = 100);

Here’s a simple Python function that you can use to create an IVFFlat index with the correct parameters for lists and probes as discussed above:

def create_ivfflat_index(conn, table_name, column_name, query_operator="<=>"): 
    index_method = "invalid"
    if query_operator == "<->":
        index_method = "vector_l2_ops"
    elif query_operator == "<#>":
        index_method = "vector_ip_ops"
    elif query_operator == "<=>":
        index_method = "vector_cosine_ops"
    else:
        raise ValueError(f"unrecognized operator {query_operator}")

    with conn.cursor() as cur:
        cur.execute(f"SELECT COUNT(*) as cnt FROM {table_name};")
        num_records = cur.fetchone()[0]

        num_lists = num_records / 1000
        if num_lists < 10:
            num_lists = 10
        if num_records > 1000000:
            num_lists = math.sqrt(num_records)

        cur.execute(f'CREATE INDEX ON {table_name} USING ivfflat ({column_name} {index_method}) WITH (lists = {num_lists});')
        conn.commit()

Querying

An index can be used whenever there is an ORDER BY of the form column <query operator> <some pseudo-constant vector> along with a LIMIT k;

Some examples

Get the closest two vectors to a constant vector:

SELECT * FROM my_table ORDER BY embedding_column <=> '[1,2]' LIMIT 2;

This is a common usage pattern in retrieval augmented generation using LLMs, where we find the embedding vectors that are closest in semantic meaning to the user’s query. In that case, the constant vector would be the embedding vector representing the user’s query.

You can see an example of this in our guide to creating, storing, and querying OpenAI embeddings with pgvector, where we use this Python function to find the three most similar documents to a given user query from our database:

# Helper function: Get top 3 most similar documents from the database
def get_top3_similar_docs(query_embedding, conn):
    embedding_array = np.array(query_embedding)
    # Register pgvector extension
    register_vector(conn)
    cur = conn.cursor()
    # Get the top 3 most similar documents using the KNN <=> operator
    cur.execute("SELECT content FROM embeddings ORDER BY embedding <=> %s LIMIT 3", (embedding_array,))
    top3_docs = cur.fetchall()
    return top3_docs

Get the closest vector to some row:

SELECT * FROM my_table WHERE id != 1 ORDER BY embedding_column <=> (SELECT embedding_column FROM my_table WHERE id = 1) LIMIT 2;

Tip: PostgreSQL's ability to use an index does not guarantee its usage! The cost-based planner evaluates query plans and may determine that a sequential scan or a different index is more efficient for a specific query. You can use the EXPLAIN command to see the chosen execution plan. To test the viability of using an index, you can modify planner costing parameters until you achieve the desired plan. For small datasets, setting enable_seqscan = 0 can be especially advantageous for testing viability as it avoids sequential scans.

To adjust the probes parameter, you can set the ivfflat.probes variable. For instance, to set it to '5', execute the following statement before running the query:

SET ivfflat.probes = 5;

Dealing with data changes

As your data evolves with inserts, updates, and deletes, the IVFFlat index will be updated accordingly. New vectors will be added to the index, while no longer-used vectors will be removed.

However, the clustering centroids will not be updated. Over time, this can result in a situation where the initial clustering, established during index creation, no longer accurately represents the data. This can be visualized as follows:

To address this issue, the only solution is to rebuild the index.

Here are two important takeaways from this issue:

• Build the index once you have all the representative data you want to reference in it. This is unlike most indexes, which can be built on an empty table.
• It is advisable to periodically rebuild the index.
  

When rebuilding the index, it is highly recommended to use the CONCURRENTLYoption to avoid interfering with ongoing operations.

Thus, to rebuild the index run the following in a cron job:

REINDEX INDEX CONCURRENTLY <index name>;

Summing It Up

The IVFFlat algorithm in pgvector provides an efficient solution for approximate nearest neighbor search over high-dimensional data like embeddings. It works by clustering similar vectors into regions and building an inverted index to map each region to its vectors. This allows queries to focus on a subset of the data, enabling fast search. By tuning the lists and probes parameters, IVFFlat can balance speed and accuracy for a dataset.

Overall, IVFFlat gives PostgreSQL the ability to perform fast semantic similarity search over complex data. With simple queries, applications can find the nearest neighbors to a query vector among millions of high-dimensional vectors. For natural language processing, information retrieval, and more, IVFFlat is a compelling solution. By understanding how IVFFlat divides the vector space into regions and builds its inverted index, you can optimize its performance for your needs and build powerful applications on top of it.

✨Resources for further learning: Now that you know more about the IVFFlat index in pgvector, here are some resources to further your learning journey: 

• Learn about other PostgreSQL indexes for vector search, like HNSW.
• Learn how we made PostgreSQL as fast as Pinecone for vector data.
• Follow our tutorial on creating, storing, and querying OpenAI embeddings using PostgreSQL as a vector database. Learn how to use pgvector as a vector store in LangChain. Or see how you can refine vector search queries using time filters in pgvector with a single SQL query.

And if you’re looking for a production-ready PostgreSQL database for your AI application’s vector, relational, and time-series data, try Timescale Cloud.